强化学习笔记（三）最优状态值与贝尔曼最优方程

强化学习的最终目标是寻找最优策略。为了实现这一目标,我们需要明确定义什么是最优策略。

本章将介绍两个核心概念:最优状态值和贝尔曼最优性方程。

最优状态值是用来定义最优策略的基础,而贝尔曼最优性方程则是求解最优状态值和最优策略的重要工具。

1. 如何改进策略?

让我们从一个简单的例子开始,来说明如何改进一个给定的策略。

考虑下图中的策略。橙色和蓝色单元格分别代表禁区和目标区域。

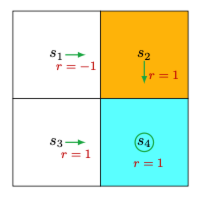
这里的策略并不好,因为它在状态s1选择了a2(向右)。那么,我们如何改进这个策略以获得更好的策略呢?

答案就在状态值和动作值中。

直观上,我们可以看出,如果策略在s1选择a3(向下)而不是a2(向右),就可以改进。这是因为向下移动可以让智能体避免进入禁区。

从数学角度来看,我们可以通过计算状态值和动作值来实现这种直觉。

首先,我们计算给定策略的状态值。特别地,这个策略的贝尔曼方程是:

\begin{align*} v_\pi(s_1) &= -1 + \gamma v_\pi(s_2) \\ v_\pi(s_2) &= +1 + \gamma v_\pi(s_4) \\ v_\pi(s_3) &= +1 + \gamma v_\pi(s_4) \\ v_\pi(s_4) &= +1 + \gamma v_\pi(s_4) \end{align*}

让 $\gamma = 0.9$ , 我们可以很容易地解出:

\begin{align*} v_\pi(s_4) &= v_\pi(s_3) = v_\pi(s_2) = 10 \\ v_\pi(s_1) &= 8 \end{align*}

其次,我们计算状态s1的动作值:

\begin{align*} q_\pi(s_1, a_1) &= -1 + \gamma v_\pi(s_1) = 6.2 \\ q_\pi(s_1, a_2) &= -1 + \gamma v_\pi(s_2) = 8 \\ q_\pi(s_1, a_3) &= 0 + \gamma v_\pi(s_3) = 9 \\ q_\pi(s_1, a_4) &= -1 + \gamma v_\pi(s_1) = 6.2 \\ q_\pi(s_1, a_5) &= 0 + \gamma v_\pi(s_1) = 7.2 \end{align*}

值得注意的是,动作a3具有最大的动作值:

q_\pi(s_1, a_3) \geq q_\pi(s_1, a_i), \text{ for all } i \neq 3

因此,我们可以更新策略,在s1选择a3。

这个例子说明,如果我们更新策略以选择具有最大动作值的动作,就可以获得更好的策略。这是许多强化学习算法的基本思想。

这个例子很简单,因为给定的策略只在状态s1不好。如果策略在其他状态也不好,选择具有最大动作值的动作是否仍然会产生更好的策略?此外,是否总是存在最优策略?最优策略是什么样的?我们将在本章回答所有这些问题。

2. 最优状态值和最优策略

虽然强化学习的最终目标是获得最优策略,但首先需要定义什么是最优策略。这个定义是基于状态值的。特别地,考虑两个给定的策略 $\pi_1$ 和 $\pi_2$ 。如果 $\pi_1$ 的状态值大于或等于 $\pi_2$ 对于任何状态的状态值:

v_{\pi_1}(s) \geq v_{\pi_2}(s), \text{ for all } s \in S

那么我们说 $\pi_1$ 比 $\pi_2$ 好。进一步,如果一个策略比所有其他可能的策略都好,那么这个策略就是最优的。

形式化的定义如下:

定义 3.1 (最优策略和最优状态值): 如果对于所有 $s \in S$ 和任何其他策略 $\pi$ ,策略 $\pi^*$ 满足 $v_{\pi^*}(s) \geq v_\pi(s)$ ,那么 $\pi^*$ 是最优的。 $\pi^*$ 的状态值是最优状态值。

这个定义表明,最优策略对每个状态都有最大的状态值,相比所有其他策略。这个定义也引出了许多问题:

存在性:最优策略是否存在?
唯一性:最优策略是否唯一?
随机性:最优策略是随机的还是确定性的?
算法:如何获得最优策略和最优状态值?

要彻底理解最优策略,必须清楚地回答这些基本问题。例如,关于最优策略的存在性,如果最优策略不存在,那么我们就不需要费心设计算法来寻找它们。我们将在本章的剩余部分回答所有这些问题。

3. 贝尔曼最优性方程

分析最优策略和最优状态值的工具是贝尔曼最优性方程(Bellman Optimality Equation, BOE)。通过求解这个方程,我们可以获得最优策略和最优状态值。

对于每个 $s \in S$ ，BOE的元素形式是:

v(s) = \max_{\pi(s)\in\Pi(s)} \sum_{a\in A} \pi(a|s) \left(\sum_{r\in R} p(r|s,a)r + \gamma \sum_{s'\in S} p(s'|s,a)v(s')\right) = \max_{\pi(s)\in\Pi(s)} \sum_{a\in A} \pi(a|s)q(s,a)

其中 $v(s)$ , $v(s')$ 是待求解的未知变量,而

q(s,a) = \sum_{r\in R} p(r|s,a)r + \gamma \sum_{s'\in S} p(s'|s,a)v(s')

这里, $\pi(s)$ 表示状态s的策略, $\Pi(s)$ 是s的所有可能策略的集合。

BOE是分析最优策略的一个优雅而强大的工具。然而,理解这个方程可能并不简单。例如,这个方程有两个未知变量 $v(s)$ 和 $\pi(a|s)$ 。初学者可能会困惑如何从一个方程中求解两个未知变量。此外,BOE实际上是一个特殊的贝尔曼方程。然而,这一点并不容易看出,因为它的表达式与普通贝尔曼方程相当不同。我们还需要回答关于BOE的以下基本问题:

存在性:这个方程是否有解?
唯一性:解是否唯一?
算法:如何求解这个方程?
最优性:解与最优策略有什么关系?

一旦我们能够回答这些问题,我们就能清楚地理解最优状态值和最优策略。

3.1 BOE右侧的最大化

接下来,我们来澄清如何解决BOE右侧的最大化问题。乍一看,初学者可能会困惑如何从一个方程中求解两个未知变量 $v(s)$ 和 $\pi(a|s)$ 。实际上,这两个未知变量可以一个接一个地求解。这个想法可以通过以下例子来说明:

示例 3.1: 考虑满足以下方程的两个未知变量 $x, y \in \mathbb{R}$ :

x = \max_{y\in\mathbb{R}} (2x - 1 - y^2)

第一步是解出右侧方程中的y。无论x的值如何,我们总是有 $\max_y (2x - 1 - y^2) = 2x - 1$ ,其中最大值在 $y = 0$ 时达到。第二步是解x。当 $y = 0$ 时,方程变为 $x = 2x - 1$ ,这导致 $x = 1$ 。因此, $y = 0$ 和 $x = 1$ 是方程的解。

现在我们来看BOE右侧的最大化问题。BOE可以简洁地写成:

v(s) = \max_{\pi(s)\in\Pi(s)} \sum_{a\in A} \pi(a|s)q(s,a), \quad s \in S

受示例3.1的启发,我们可以首先解出右侧的最优 $\pi$ 。如何做到这一点?以下示例演示了其基本思想:

示例 3.2: 给定 $q_1, q_2, q_3 \in \mathbb{R}$ ,我们想要找到 $c_1, c_2, c_3$ 的最优值以最大化:

\sum_{i=1}^3 c_i q_i = c_1 q_1 + c_2 q_2 + c_3 q_3

其中 $c_1 + c_2 + c_3 = 1$ 且 $c_1, c_2, c_3 \geq 0$ 。

不失一般性,假设 $q_3 \geq q_1, q_2$ 。那么,最优解是 $c_3^* = 1$ 且 $c_1^* = c_2^* = 0$ 。这是因为对于任何 $c_1, c_2, c_3$ ,都有:

q_3 = (c_1 + c_2 + c_3)q_3 = c_1 q_3 + c_2 q_3 + c_3 q_3 \geq c_1 q_1 + c_2 q_2 + c_3 q_3

受上述示例的启发,由于 $\sum_a \pi(a|s) = 1$ ,我们有:

\sum_{a\in A} \pi(a|s)q(s,a) \leq \sum_{a\in A} \pi(a|s) \max_{a\in A} q(s,a) = \max_{a\in A} q(s,a)

其中等号在以下情况下成立:

\pi(a|s) = \begin{cases} 1, & a = a^* \\ 0, & a \neq a^* \end{cases}

这里, $a^* = \arg\max_a q(s,a)$ 。总之,最优策略 $\pi(s)$ 是选择具有最大 $q(s,a)$ 值的动作。

3.2 BOE的矩阵-向量形式

BOE指的是为所有状态定义的一组方程。如果我们将这些方程组合起来,我们可以得到一个简洁的矩阵-向量形式,这将在本章中被广泛使用。

BOE的矩阵-向量形式是:

v = \max_{\pi\in\Pi} (r_\pi + \gamma P_\pi v)

其中 $v \in \mathbb{R}^{|S|}$ ,且 $\max_\pi$ 以元素方式执行。 $r_\pi$ 和 $P_\pi$ 的结构与普通贝尔曼方程的矩阵-向量形式相同:

[r_\pi]_s = \sum_{a\in A} \pi(a|s) \sum_{r\in R} p(r|s,a)r, \quad [P_\pi]_{s,s'} = p(s'|s) = \sum_{a\in A} \pi(a|s)p(s'|s,a)

由于 $\pi$ 的最优值由 $v$ 决定,方程右侧是 $v$ 的函数,记为:

f(v) = \max_{\pi\in\Pi} (r_\pi + \gamma P_\pi v)

然后,BOE可以以简洁的形式表示为:

v = f(v)

在本节的剩余部分,我们将展示如何解这个非线性方程。

3.3 收缩映射定理

由于BOE可以表示为非线性方程 $v = f(v)$ ,我们接下来介绍收缩映射定理来分析它。收缩映射定理是分析一般非线性方程的强大工具。它也被称为不动点定理。

考虑函数 $f(x)$ ,其中 $x \in \mathbb{R}^d$ 且 $f: \mathbb{R}^d \rightarrow \mathbb{R}^d$ 。如果点 $x^*$ 满足: $f(x^*) = x^*$ ，则称 $x^*$ 为不动点。这个方程的解释是 $x^*$ 的映射是它自己。这就是为什么 $x^*$ 被称为"不动"的原因。

如果存在 $\gamma \in (0,1)$ 使得对于任何 $x_1, x_2 \in \mathbb{R}^d$ ,都有:

\|f(x_1) - f(x_2)\| \leq \gamma\|x_1 - x_2\|

则函数 $f$ 是一个收缩映射(或收缩函数)。这里 $\|\cdot\|$ 表示向量或矩阵范数。

以下定理描述了不动点和收缩性质之间的关系:

定理 3.1 (收缩映射定理): 对于任何形式为 $x = f(x)$ 的方程,其中 $x$ 和 $f(x)$ 是实向量,如果 $f$ 是一个收缩映射,则以下性质成立:

存在性: 存在一个不动点 $x^*$ 满足 $f(x^*) = x^*$ 。
唯一性: 不动点 $x^*$ 是唯一的。
算法: 考虑迭代过程:

$x_{k+1} = f(x_k)$

其中 $k = 0, 1, 2, ...$ 。那么对于任何初始猜测 $x_0$ ,都有 $x_k \rightarrow x^*$ 当 $k \rightarrow \infty$ 。而且,收敛速度是指数级的。

收缩映射定理不仅可以告诉我们非线性方程的解是否存在,还提供了一种求解方程的数值算法。

3.4 BOE右侧的收缩性质

接下来,我们证明BOE中的 $f(v)$ 是一个收缩映射。因此,我们可以应用前面介绍的收缩映射定理。

定理 3.2 (f(v)的收缩性质): BOE右侧的函数 $f(v)$ 是一个收缩映射。特别地,对于任何 $v_1, v_2 \in \mathbb{R}^{|S|}$ ,都有:

\|f(v_1) - f(v_2)\|_\infty \leq \gamma\|v_1 - v_2\|_\infty

其中 $\gamma \in (0,1)$ 是折扣率, $\|\cdot\|_\infty$ 是最大范数,即向量元素的最大绝对值。

这个定理很重要,因为我们可以用强大的收缩映射定理来分析BOE。

4. 从BOE求解最优策略

有了前面的准备,我们现在准备求解BOE以获得最优状态值 $v^*$ 和最优策略 $\pi^*$ 。

求解 $v^*$ : 如果 $v^*$ 是BOE的解,那么它满足:

v^* = \max_{\pi\in\Pi} (r_\pi + \gamma P_\pi v^*)

显然, $v^*$ 是一个不动点,因为 $v^* = f(v^*)$ 。然后,收缩映射定理建议以下结果:

定理 3.3 (存在性、唯一性和算法): 对于BOE $v = f(v) = \max_{\pi\in\Pi}(r_\pi + \gamma P_\pi v)$ ,总是存在唯一的解 $v^*$ ,可以通过以下迭代算法求解:

v_{k+1} = f(v_k) = \max_{\pi\in\Pi} (r_\pi + \gamma P_\pi v_k), \quad k = 0, 1, 2, ...

给定任何初始猜测 $v_0$ ， $v_k$ 的值以指数速度收敛到 $v^*$ 当 $k \rightarrow \infty$ 。

这个定理的证明直接来自收缩映射定理,因为 $f(v)$ 是一个收缩映射。这个定理很重要,因为它回答了一些基本问题:

$v^*$ 的存在性: BOE的解总是存在。
$v^*$ 的唯一性: 解 $v^*$ 总是唯一的。
求解 $v^*$ 的算法: $v^*$ 的值可以通过定理3.3建议的迭代算法求解。这个迭代算法有一个特定的名称叫做值迭代。它的实现将在第4章详细介绍。
求解 $\pi^*$ : 一旦获得了 $v^*$ 的值,我们可以很容易地通过求解以下问题获得 $\pi^*$ :

\pi^* = \arg\max_{\pi\in\Pi} (r_\pi + \gamma P_\pi v^*)

$\pi^*$ 的值将在定理3.5中给出。将上式代入BOE得到:

v^* = r_{\pi^*} + \gamma P_{\pi^*} v^*

因此, $v^* = v_{\pi^*}$ 是 $\pi^*$ 的状态值,BOE是一个特殊的贝尔曼方程,其对应的策略是 $\pi^*$ 。

虽然我们现在可以求解 $v^*$ 和 $\pi^*$ ,但仍不清楚解是否是最优的。以下定理揭示了解的最优性:

定理 3.4 ( $v^*$ 和 $\pi^*$ 的最优性): 解 $v^*$ 是最优状态值, $\pi^*$ 是最优策略。也就是说,对于任何策略 $\pi$ ,都有:

v^* = v_{\pi^*} \geq v_\pi

其中 $v_\pi$ 是 $\pi$ 的状态值,≥是元素比较。

现在很清楚为什么我们必须研究BOE: 它的解对应于最优状态值和最优策略。

接下来,我们更仔细地检查 $\pi^*$ 。特别地,以下定理表明总是存在确定性的贪婪策略是最优的:

定理 3.5 (贪婪最优策略): 对于任何 $s \in S$ ,确定性贪婪策略

\pi^*(a|s) = \begin{cases} 1, & a = a^*(s) \\ 0, & a \neq a^*(s) \end{cases}

是求解BOE的最优策略。这里,

a^*(s) = \arg\max_a q^*(a,s)

其中

q^*(s,a) = \sum_{r\in R} p(r|s,a)r + \gamma \sum_{s'\in S} p(s'|s,a)v^*(s')

最后,我们讨论 $\pi^*$ 的两个重要性质:

最优策略的唯一性: 虽然 $v^*$ 的值是唯一的,但对应于 $v^*$ 的最优策略可能不是唯一的。
最优策略的随机性: 最优策略可以是随机的,也可以是确定性的。然而,根据定理3.5,可以确定总是存在一个确定性的最优策略。

5. 影响最优策略的因素

BOE是分析最优策略的强大工具。我们可以通过观察BOE的元素表达式来研究哪些因素可以影响最优策略:

v(s) = \max_{\pi(s)\in\Pi(s)} \sum_{a\in A} \pi(a|s) \left(\sum_{r\in R} p(r|s,a)r + \gamma \sum_{s'\in S} p(s'|s,a)v(s')\right), \quad s \in S

最优状态值和最优策略由以下参数决定: 1) 即时奖励 $r$ , 2) 折扣率 $\gamma$ , 3) 系统模型 $p(s'|s,a), p(r|s,a)$ 。虽然系统模型是固定的,但我们可以讨论当我们改变 $r$ 和 $\gamma$ 的值时,最优策略如何变化。

5.1 折扣率的影响

如果我们将折扣率从 $\gamma = 0.9$ 改为 $\gamma = 0.5$ ,并保持其他参数不变,最优策略会变得更加短视。也就是说,智能体不敢冒险,即使这样做可能会在之后获得更大的累积奖励。

在极端情况下,如果 $\gamma = 0$ ,结果得到的最优策略会变得非常短视。智能体会选择具有最大即时奖励的动作,即使从长远来看该动作并不好。

5.2 奖励值的影响

如果我们想严格禁止智能体进入任何禁区,我们可以增加进入禁区的惩罚。例如,如果我们将 $r_{forbidden}$ 从-1改为-10,得到的最优策略就可以避开所有禁区。

然而,改变奖励并不总是导致不同的最优策略。一个重要的事实是,最优策略对奖励的仿射变换是不变的。换句话说,如果我们按比例缩放所有奖励或对所有奖励加上相同的值,最优策略保持不变。

定理 3.6 (最优策略不变性): 考虑一个马尔可夫决策过程,其最优状态值 $v^* \in \mathbb{R}^{|S|}$ 满足 $v^* = \max_{\pi\in\Pi}(r_\pi + \gamma P_\pi v^*)$ 。如果每个奖励 $r \in R$ 通过仿射变换变为 $\alpha r + \beta$ ,其中 $\alpha, \beta \in \mathbb{R}$ 且 $\alpha > 0$ ,那么对应的最优状态值 $v'$ 也是 $v^*$ 的仿射变换:

v' = \alpha v^* + \frac{\beta}{1-\gamma} \mathbf{1}

其中 $\gamma \in (0,1)$ 是折扣率, $\mathbf{1} = [1, ..., 1]^T$ 。因此,从 $v'$ 导出的最优策略对奖励值的仿射变换是不变的。

5.3 避免无意义的绕路

在奖励设置中,智能体在每一步移动时都会收到奖励 $r_{other} = 0$ （除非它进入禁区或目标区域或尝试超出边界）。由于零奖励不是惩罚,最优策略是否会在到达目标之前采取无意义的绕路?我们是否应该将 $r_{other}$ 设为负值以鼓励智能体尽快到达目标?

事实上,虽然每一步的即时奖励并不鼓励智能体尽快接近目标,但折扣率确实鼓励这样做。这是因为,尽管绕路可能不会收到任何即时负奖励,但它会增加轨迹长度并减少折扣回报。

初学者可能会误解,认为在每一步的奖励基础上添加一个负奖励（例如,-1）是必要的,以鼓励智能体尽快到达目标。这是一个误解,因为在所有奖励之上添加相同的奖励是一个仿射变换,它保持最优策略不变。此外,由于折扣率的存在,最优策略不会采取无意义的绕路,即使绕路可能不会收到任何即时负奖励。

目录