在强化学习中,评估一个策略的好坏是至关重要的。本章将介绍两个核心概念:状态值和贝尔曼方程,它们是评估策略的基础工具。状态值被定义为智能体遵循给定策略时能够获得的平均奖励。状态值越大,相应的策略就越好。因此,状态值可以作为衡量策略好坏的指标。
然而,仅仅知道状态值的重要性是不够的,我们还需要知道如何分析它们。这就是贝尔曼方程发挥作用的地方。贝尔曼方程是分析状态值的重要工具,它描述了所有状态值之间的关系。通过求解贝尔曼方程,我们可以获得状态值。这个过程被称为策略评估,是强化学习中的一个基本概念。
本章将深入探讨这些概念,从简单的例子开始,逐步引入更复杂的数学表达。我们将学习如何构建贝尔曼方程,如何求解它,以及如何解释结果。此外,本章还将介绍另一个重要概念:动作值,并探讨它与状态值之间的关系。
1. 为什么要关注回报?
首先我们来看一个简单的例子,说明回报(return)的重要性:
考虑下面三种不同的策略:
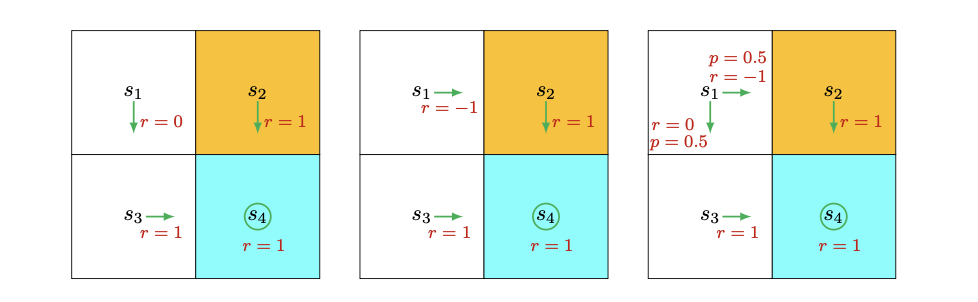
直观上看,左边的策略是最好的,因为从s1开始的智能体可以避开禁区。中间的策略看起来最差,因为从s1开始会直接进入禁区。右边的策略介于两者之间,有0.5的概率进入禁区。
那么如何用数学的方式来描述这种直观判断呢?答案就是使用回报的概念。
假设智能体从s1开始,折扣率为γ (0<γ<1):
- 按照第一个策略,轨迹为 s1→s3→s4→s4...,折扣回报为:
return1=0+γ1+γ21+...=1−γγ
- 按照第二个策略,轨迹为 s1→s2→s4→s4...,折扣回报为:
return2=−1+γ1+γ21+...=−1+1−γγ
- 按照第三个策略,有两种可能的轨迹,各自概率为0.5:
s1→s3→s4→s4...
s1→s2→s4→s4...
平均折扣回报为:
return3=0.5(−1+1−γγ)+0.5(1−γγ)=−0.5+1−γγ
比较三个策略的回报,我们可以发现:
return1>return3>return2
这个数学结论与我们之前的直观判断是一致的:第一个策略最好,因为可以避开禁区;第二个策略最差,因为会直接进入禁区。
这个例子说明,回报可以用来评估策略的好坏:回报越高,策略越好。
2. 如何计算回报?
既然回报如此重要,那么如何计算回报呢?有两种方法:
2.1 直接按定义计算
回报等于沿着轨迹收集到的所有奖励的折扣和。考虑下面的例子:
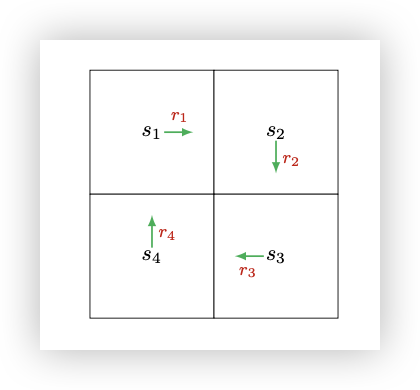
假设vi表示从si开始获得的回报,则:
v1v2v3v4=r1+γr2+γ2r3+...=r2+γr3+γ2r4+...=r3+γr4+γ2r1+...=r4+γr1+γ2r2+...
2.2 基于自举法计算
观察上面的表达式,我们可以重写为:
v1v2v3v4=r1+γ(r2+γr3+...)=r1+γv2=r2+γ(r3+γr4+...)=r2+γv3=r3+γ(r4+γr1+...)=r3+γv4=r4+γ(r1+γr2+...)=r4+γv1
这些方程表明回报值之间存在相互依赖关系,这反映了自举法的思想:从自身获取某些量的值。
从数学角度看,这些方程可以改写成一个线性矩阵-向量方程:
⎣⎡v1v2v3v4⎦⎤=⎣⎡r1r2r3r4⎦⎤+γ⎣⎡0001100001000010⎦⎤⎣⎡v1v2v3v4⎦⎤
简洁表示为:
v=r+γPv
其中v可以通过求解:v=(I−γP)−1r 得到。
这个简单的例子展示了贝尔曼方程的核心思想:从一个状态开始获得的回报取决于从其他状态开始获得的回报。
3. 状态值
虽然回报可以用来评估策略,但它在随机系统中并不适用,因为从一个状态开始可能导致不同的回报。为了解决这个问题,我们引入状态值的概念。
首先引入一些必要的符号。考虑一系列时间步t=0,1,2,...。在时间t,智能体处于状态St,按照策略π采取动作At。下一个状态是St+1,获得的即时奖励是Rt+1。这个过程可以简洁地表示为:
StAtSt+1,Rt+1
注意St, St+1, At, Rt+1都是随机变量。
从t开始,我们可以得到一个状态-动作-奖励轨迹:
StAtSt+1,Rt+1At+1St+2,Rt+2At+2St+3,Rt+3...
根据定义,沿着这个轨迹的折扣回报是:
Gt≐Rt+1+γRt+2+γ2Rt+3+...
其中γ∈(0,1)是折扣率。注意Gt是一个随机变量,因为Rt+1,Rt+2,...都是随机变量。
由于Gt是一个随机变量,我们可以计算它的期望值:
vπ(s)≐E[Gt∣St=s]
这里,vπ(s)被称为状态值函数,或简称为状态s的状态值。
关于状态值,有以下几个重要的说明:
-
vπ(s)依赖于s。这是因为它的定义是一个条件期望,条件是智能体从St=s开始。
-
vπ(s)依赖于π。这是因为轨迹是通过遵循策略π生成的。对于不同的策略,状态值可能不同。
-
vπ(s)不依赖于t。如果智能体在状态空间中移动,t表示当前的时间步。一旦给定策略,vπ(s)的值就确定了。
状态值与回报的关系可以进一步说明如下:当策略和系统模型都是确定性的时候,从一个状态开始总是会导致相同的轨迹。在这种情况下,从一个状态开始获得的回报等于该状态的值。相比之下,当策略或系统模型是随机的时候,从同一个状态开始可能会生成不同的轨迹。在这种情况下,不同轨迹的回报是不同的,而状态值是这些回报的平均值。
虽然回报可以用来评估策略,但使用状态值来评估策略更加正式:产生更大状态值的策略更好。因此,状态值构成了强化学习中的一个核心概念。
4. 贝尔曼方程
既然状态值如此重要,那么如何计算它们呢?这个问题的答案就是贝尔曼方程,它是分析状态值的数学工具。简而言之,贝尔曼方程是一组描述所有状态值之间关系的线性方程。
我们现在来推导贝尔曼方程。首先,注意到Gt可以重写为:
Gt=Rt+1+γRt+2+γ2Rt+3+...=Rt+1+γ(Rt+2+γRt+3+...)=Rt+1+γGt+1
其中Gt+1=Rt+2+γRt+3+...。这个方程建立了Gt和Gt+1之间的关系。然后,状态值可以写为:
vπ(s)=E[Gt∣St=s]=E[Rt+1+γGt+1∣St=s]=E[Rt+1∣St=s]+γE[Gt+1∣St=s]
方程中的两项可以分别分析:
-
第一项E[Rt+1∣St=s]是即时奖励的期望。使用全期望定律,它可以计算为:
E[Rt+1∣St=s]=a∈A∑π(a∣s)E[Rt+1∣St=s,At=a]=a∈A∑π(a∣s)r∈R∑p(r∣s,a)r
这里,A和R分别是可能的动作和奖励的集合。
-
第二项E[Gt+1∣St=s]是未来奖励的期望。它可以计算为:
E[Gt+1∣St=s]=s′∈S∑E[Gt+1∣St=s,St+1=s′]p(s′∣s)=s′∈S∑E[Gt+1∣St+1=s′]p(s′∣s)(由于马尔可夫性质)=s′∈S∑vπ(s′)p(s′∣s)=s′∈S∑vπ(s′)a∈A∑p(s′∣s,a)π(a∣s)
将这两项代入原方程,我们得到贝尔曼方程:
vπ(s)=a∈A∑π(a∣s)[r∈R∑p(r∣s,a)r+γs′∈S∑p(s′∣s,a)vπ(s′)],∀s∈S
这个方程看起来很复杂,但实际上它有清晰的结构。以下是一些说明:
-
vπ(s)和vπ(s′)是要计算的未知状态值。初学者可能会感到困惑,如何计算未知的vπ(s),因为它依赖于另一个未知的vπ(s′)。必须注意的是,贝尔曼方程指的是对所有状态的一组线性方程,而不是单个方程。如果我们把这些方程放在一起,就清楚如何计算所有的状态值了。
-
π(a∣s)是给定的策略。由于状态值可以用来评估策略,从贝尔曼方程求解状态值是一个策略评估过程,这是许多强化学习算法中的重要过程。
-
p(r∣s,a)和p(s′∣s,a)表示系统模型。
除了上面的表达式,贝尔曼方程还有其他等价的表达形式。例如:
vπ(s)=a∈A∑π(a∣s)s′∈S∑r∈R∑p(s′,r∣s,a)[r+γvπ(s′)]
或者,如果奖励只依赖于下一个状态s′,我们可以写成:
vπ(s)=a∈A∑π(a∣s)s′∈S∑p(s′∣s,a)[r(s′)+γvπ(s′)]
4.1 贝尔曼方程的例子
让我们通过两个例子来演示如何写出贝尔曼方程并逐步计算状态值。
例1:确定性策略
考虑图4.1中的确定性策略。
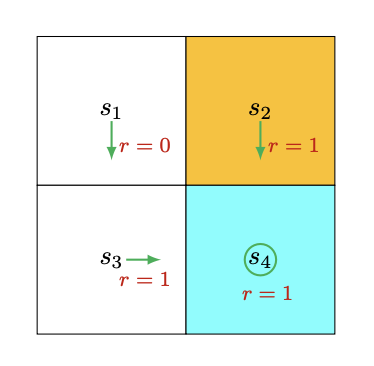
对于状态s1,在该策略下,采取动作的概率为π(a=a3∣s1)=1和π(a=a3∣s1)=0。状态转移概率为p(s′=s3∣s1,a3)=1和p(s′=s3∣s1,a3)=0。奖励概率为p(r=0∣s1,a3)=1和p(r=0∣s1,a3)=0。
将这些值代入贝尔曼方程,我们得到:
vπ(s1)=0+γvπ(s3)
类似地,我们可以得到:
vπ(s2)vπ(s3)vπ(s4)=1+γvπ(s4)=1+γvπ(s4)=1+γvπ(s4)
解这些方程,我们可以得到:
vπ(s4)vπ(s3)vπ(s2)vπ(s1)=1−γ1=1−γ1=1−γ1=1−γγ
如果我们设γ=0.9,那么:
vπ(s4)vπ(s3)vπ(s2)vπ(s1)=10=10=10=9
例2:随机策略
现在考虑图4.2中的随机策略。
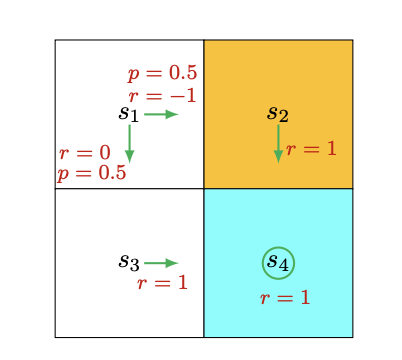
在状态s1,向右和向下的概率都是0.5。数学上,我们有π(a=a2∣s1)=0.5和π(a=a3∣s1)=0.5。状态转移概率是确定的,因为p(s′=s3∣s1,a3)=1和p(s′=s2∣s1,a2)=1。奖励概率也是确定的,因为p(r=0∣s1,a3)=1和p(r=−1∣s1,a2)=1。
将这些值代入贝尔曼方程,我们得到:
vπ(s1)=0.5[0+γvπ(s3)]+0.5[−1+γvπ(s2)]
类似地,我们可以得到:
vπ(s2)vπ(s3)vπ(s4)=1+γvπ(s4)=1+γvπ(s4)=1+γvπ(s4)
解这些方程,我们可以得到:
vπ(s4)vπ(s3)vπ(s2)vπ(s1)=1−γ1=1−γ1=1−γ1=−0.5+1−γγ
如果我们设γ=0.9,那么:
vπ(s4)vπ(s3)vπ(s2)vπ(s1)=10=10=10=8.5
如果我们比较这两个策略的状态值,可以看到:
vπ1(si)≥vπ2(si),i=1,2,3,4
这表明图4.1中的策略更好,因为它有更大的状态值。这个数学结论与我们的直觉一致:第一个策略更好,因为当智能体从s1开始时,它可以避免进入禁区。
这两个例子展示了如何使用贝尔曼方程来计算状态值,并且说明了状态值如何可以用来评估策略的好坏。在接下来的章节中,我们将看到如何利用这些概念来开发和分析各种强化学习算法。
5. 贝尔曼方程的矩阵-向量形式
贝尔曼方程的元素形式对于每个状态都是有效的,我们可以将所有这些方程组合起来,以矩阵-向量形式简洁地表示:
vπ=rπ+γPπvπ
其中:
- vπ=[vπ(s1),...,vπ(sn)]T∈Rn
- rπ=[rπ(s1),...,rπ(sn)]T∈Rn
- Pπ∈Rn×n,其中 [Pπ]ij=pπ(sj∣si)
矩阵Pπ有一些有趣的性质:
- 它是一个非负矩阵,即所有元素都大于或等于零。
- 它是一个随机矩阵,即每行的和等于1。
6. 从贝尔曼方程求解状态值
计算给定策略的状态值是强化学习中的一个基本问题,通常被称为策略评估。我们有两种方法可以从贝尔曼方程计算状态值。
6.1 闭式解
由于vπ=rπ+γPπvπ是一个简单的线性方程,其闭式解可以很容易地得到:
vπ=(I−γPπ)−1rπ
(I−γPπ)−1有一些重要的性质:
- I−γPπ总是可逆的。
- (I−γPπ)−1≥I,意味着(I−γPπ)−1的每个元素都是非负的,且不小于单位矩阵的相应元素。
- 对于任何非负向量r,都有(I−γPπ)−1r≥r≥0。
6.2 迭代解法
尽管闭式解对理论分析很有用,但在实践中并不适用,因为它涉及矩阵求逆运算,这仍然需要通过其他数值算法来计算。实际上,我们可以直接使用以下迭代算法求解贝尔曼方程:
vk+1=rπ+γPπvk,k=0,1,2,...
这个算法生成一个值序列{v0,v1,v2,...},其中v0∈Rn是vπ的初始猜测。可以证明:
vk→vπ=(I−γPπ)−1rπ,as k→∞
7. 从状态值到动作值
到目前为止,我们一直在讨论状态值,现在我们来看看动作值,它表示在一个状态下采取一个动作的"价值"。动作值的概念虽然重要,但它在很大程度上依赖于状态值的概念。
状态-动作对(s,a)的动作值定义为:
qπ(s,a)≐E[Gt∣St=s,At=a]
动作值和状态值之间有什么关系呢?
-
首先,根据条件期望的性质,我们有:
vπ(s)=a∈A∑π(a∣s)qπ(s,a)
因此,一个状态的值是与该状态相关的动作值的期望。
-
其次,由于状态值由下式给出:
vπ(s)=a∈A∑π(a∣s)[r∈R∑p(r∣s,a)r+γs′∈S∑p(s′∣s,a)vπ(s′)]
将其与上面的等式比较,我们得到:
qπ(s,a)=r∈R∑p(r∣s,a)r+γs′∈S∑p(s′∣s,a)vπ(s′)
可以看出,动作值由两部分组成:即时奖励的平均值和未来奖励的平均值。
这两个等式描述了状态值和动作值之间的关系。它们是同一枚硬币的两面:第一个等式显示了如何从动作值获得状态值,而第二个等式显示了如何从状态值获得动作值。
7.1 动作值的贝尔曼方程
我们之前介绍的贝尔曼方程是基于状态值定义的。实际上,它也可以用动作值来表示。
特别地,将vπ(s)=∑a∈Aπ(a∣s)qπ(s,a)代入qπ(s,a)的表达式,我们得到:
qπ(s,a)=r∈R∑p(r∣s,a)r+γs′∈S∑p(s′∣s,a)a′∈A(s′)∑π(a′∣s′)qπ(s′,a′)
这是一个关于动作值的方程。上面的方程对每个状态-动作对都是有效的。如果我们把所有这些方程放在一起,它们的矩阵-向量形式是:
qπ=r~+γPΠqπ
其中:
- qπ是由状态-动作对索引的动作值向量:其(s,a)th元素是[qπ](s,a)=qπ(s,a)。
- r~是由状态-动作对索引的即时奖励向量:[r~](s,a)=∑r∈Rp(r∣s,a)r。
- 矩阵P是概率转移矩阵,其行由状态-动作对索引,列由状态索引:[P](s,a),s′=p(s′∣s,a)。
- Π是一个分块对角矩阵,其中每个块是一个1×∣A∣向量:Πs′,(s′,a′)=π(a′∣s′),Π的其他条目为零。
与基于状态值定义的贝尔曼方程相比,基于动作值定义的方程有一些独特的特征。例如,r~和P独立于策略,仅由系统模型决定。策略嵌入在Π中。可以验证,这个方程也是一个压缩映射,有一个唯一的解,可以通过迭代求解。
8. 总结
本章介绍的最重要的概念是状态值。从数学上讲,状态值是智能体从一个状态开始可以获得的期望回报。不同状态的值是相互关联的,即状态s的值依赖于其他一些状态的值,而这些状态的值可能又依赖于状态s本身的值。这种现象可能是本章中最让初学者困惑的部分。它与一个重要的概念"自举"有关,自举涉及从自身计算某些东西。尽管自举在直观上可能令人困惑,但如果我们检查贝尔曼方程的矩阵-向量形式,就会发现它是清晰的。特别地,贝尔曼方程是一组描述所有状态值之间关系的线性方程。
由于状态值可以用来评估策略的好坏,从贝尔曼方程求解策略的状态值的过程被称为策略评估。正如我们将在本书后面看到的,策略评估是许多强化学习算法中的一个重要步骤。
另一个重要的概念,动作值,被引入来描述在一个状态下采取一个动作的价值。正如我们将在本书后面看到的,当我们试图找到最优策略时,动作值比状态值起着更直接的作用。
最后,贝尔曼方程并不局限于强化学习领域。相反,它广泛存在于许多领域,如控制理论和运筹学。在不同的领域,贝尔曼方程可能有不同的表达式。在本书中,贝尔曼方程是在离散马尔可夫决策过程下研究的。
通过理解这些基本概念和工具,我们为深入研究强化学习奠定了坚实的基础。在接下来的章节中,我们将看到如何利用这些概念来开发和分析各种强化学习算法。



