强化学习是机器学习的一个重要分支，它研究如何通过与环境的交互来学习最优决策策略。与监督学习和无监督学习不同，强化学习的特点在于它强调学习过程中的序列决策和长期回报。

在这一章中，我们将从最基本的概念开始，逐步构建强化学习的理论框架。我们将介绍状态、动作、策略、奖励等核心概念，并最终引入马尔可夫决策过程（MDPs）这一描述强化学习问题的数学工具。为了使这些抽象的概念更加直观，我们将使用一个简单的网格世界例子来阐述这些概念。这个例子虽然简单，但它包含了强化学习中的许多关键元素，可以帮助我们理解更复杂的问题。

1. 网格世界示例

为了更直观地理解强化学习的基本概念，我们先来看一个简单的网格世界示例。想象一个机器人(智能体)在一个3x3的网格世界中移动，其中有些格子是禁止进入的，还有一个目标格子。机器人的任务是从任意起始位置出发,找到一条到达目标格子的最优路径,同时避开禁止区域和不必要的绕路。

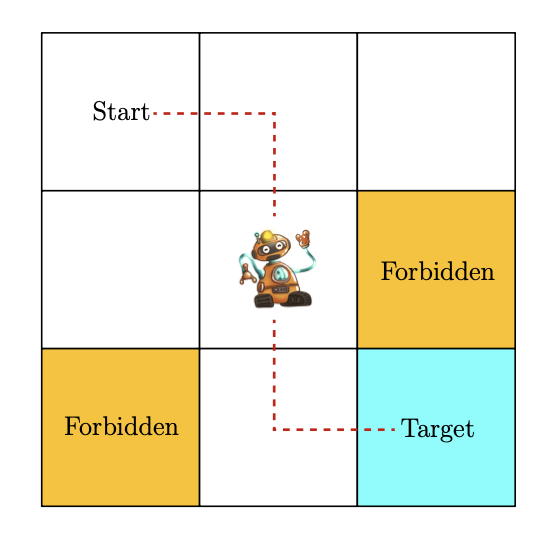
2. 状态(State)和动作(Action)

状态是描述智能体在环境中所处位置或状况的概念。在网格世界中,状态就对应着机器人所在的格子位置。我们可以用$s_1, s_2, ..., s_9$来表示这9个状态。所有可能的状态构成了状态空间$S = \{s_1, ..., s_9\}$。

动作则是智能体可以采取的行为。在这个例子中，机器人在每个状态下都有5种可能的动作:向上移动、向右移动、向下移动、向左移动以及保持不动。我们用$a_1, a_2, ..., a_5$来表示这5个动作。所有可能的动作构成了动作空间$A = \{a_1, ..., a_5\}$。

需要注意的是,不同的状态可能有不同的动作空间。比如在边界格子$s_1$，向上($a_1$)或向左($a_4$)移动会导致碰壁，因此$s_1$的动作空间可能只包含$\{a_2, a_3, a_5\}$。但为了简化问题，我们通常假设所有状态的动作空间都是相同的。

3. 状态转移(State Transition)

当智能体在某个状态下执行一个动作后,它会从当前状态转移到下一个状态,这个过程称为状态转移。例如,如果机器人在$s_1$状态下执行向右移动($a_2$)的动作,它就会转移到$s_2$状态,我们可以表示为:$s_1 \xrightarrow{a_2} s_2$。

状态转移可以用条件概率来描述。例如,$p(s_2|s_1, a_2) = 1$表示在$s_1$状态下执行$a_2$动作后,转移到$s_2$状态的概率为1。在确定性环境中,状态转移是确定的,但在随机环境中,状态转移可能是概率性的。

4. 策略(Policy)

策略是智能体在每个状态下选择动作的方法。直观上,我们可以把策略想象成一系列箭头,指示智能体在每个状态下应该采取什么动作。

数学上,策略可以用条件概率$\pi(a|s)$来表示,它表示在状态$s$下选择动作$a$的概率。例如,$\pi(a_2|s_1) = 1$表示在$s_1$状态下一定会选择$a_2$动作。

策略可以是确定性的,即在每个状态下只选择一个特定的动作;也可以是随机性的,即在一个状态下可能以不同的概率选择不同的动作。

5. 奖励(Reward)

奖励是强化学习中最独特的概念之一。智能体在执行动作后,会从环境中获得一个奖励信号$r$,这个奖励是状态$s$和动作$a$的函数,记作$r(s,a)$。奖励可以是正数、负数或零。

在网格世界例子中,我们可以这样设计奖励:

• 如果智能体试图越界,奖励为-1 ($r_{boundary} = -1$)
• 如果智能体试图进入禁止区域,奖励为-1 ($r_{forbidden} = -1$)
• 如果智能体到达目标状态,奖励为+1 ($r_{target} = +1$)
• 其他情况下,奖励为0 ($r_{other} = 0$)

奖励机制可以看作是人机交互的接口,通过它我们可以引导智能体按照我们期望的方式行动。设计合适的奖励函数是强化学习中的一个关键步骤,虽然有时候并不容易,但通常比直接解决问题要简单得多。

6. 轨迹(Trajectory)、回报(Return)和回合(Episode)

轨迹是智能体与环境交互过程中形成的状态-动作-奖励链。例如,按照某个策略,智能体可能会形成这样一条轨迹:

回报是沿着轨迹收集到的所有奖励之和。对于上面的轨迹,回报就是$0 + 0 + 0 + 1 = 1$。回报也被称为总奖励或累积奖励。

我们可以用回报来评估策略的好坏。回报越高,说明策略越好。但需要注意的是,回报包括即时奖励和未来奖励,因此在做决策时不能只看即时奖励,而应该考虑长期的累积回报。

对于无限长的轨迹,我们引入折扣回报的概念:

其中$\gamma \in (0,1)$是折扣率。折扣率的引入有两个好处:一是避免了无限长轨迹的回报发散,二是可以通过调整$\gamma$来控制智能体对近期和远期奖励的重视程度。

回合(Episode)是指从初始状态开始,到达某个终止状态的完整轨迹。有终止状态的任务称为回合式任务(Episodic tasks),没有终止状态的任务称为持续式任务(Continuing tasks)。

7. 马尔可夫决策过程(Markov Decision Processes, MDPs)

马尔可夫决策过程是描述强化学习问题的一般框架。一个MDP包含以下几个关键要素:

• 状态空间$S$
• 动作空间$A(s)$,对每个状态$s \in S$都有一个对应的动作集
• 奖励集$R(s,a)$,对每个状态-动作对$(s,a)$都有一个对应的奖励集
• 状态转移概率$p(s'|s,a)$,表示在状态$s$下执行动作$a$后转移到状态$s'$的概率
• 奖励概率$p(r|s,a)$,表示在状态$s$下执行动作$a$后获得奖励$r$的概率
• 策略$\pi(a|s)$,表示在状态$s$下选择动作$a$的概率

MDP的一个重要特性是马尔可夫性(Markov property), 即下一个状态和奖励只依赖于当前的状态和动作,与之前的历史无关:

这个性质对于推导强化学习的基本方程(如Bellman方程)非常重要。

8. 补充说明

• 奖励的设计：奖励的设计可以是相对的。例如，我们可以给所有奖励值加上一个常数，不会改变最优策略。

• 奖励与下一个状态的关系：虽然我们通常将奖励表示为$r(s,a)$，但实际上奖励也可能依赖于下一个状态$s'$。我们可以通过$p(r|s,a) = \sum_{s'} p(r|s,a,s')p(s'|s,a)$来将其转换为只依赖于$s$和$a$的形式。