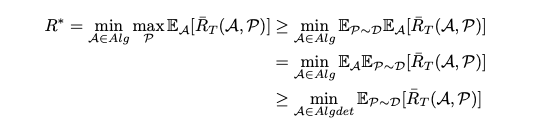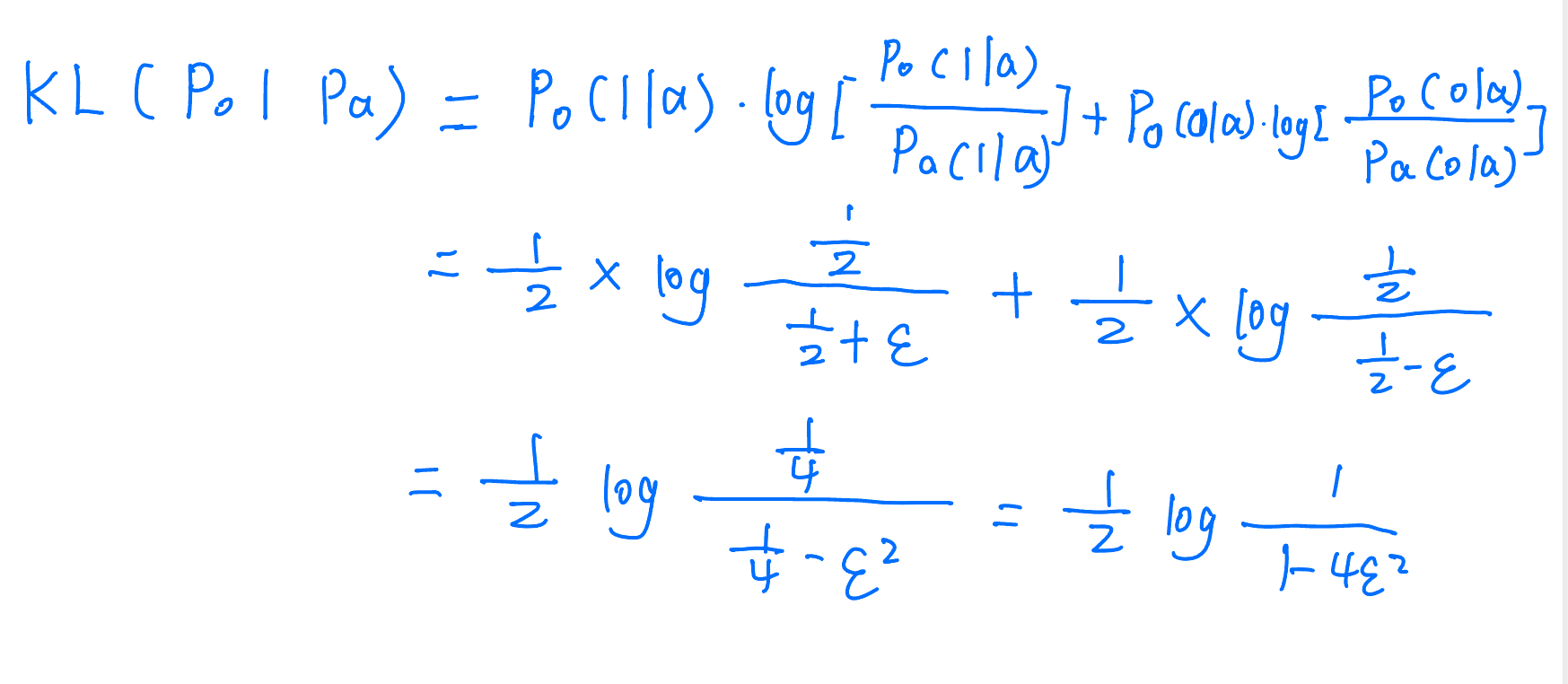前言

最近在申请Ph.D, 有幸和导师还算聊得来，老师让我先去研究一下他的官网上关于在线决策的课程，因为这对我来说是个全新的领域，所以我参考了网上关于MAB问题的一些教程和老师给的官方课件，写了一篇总结，和兄弟们一起学习一下。

⚠️：很多观点来源于本人对课件以及教程的理解，很多地方还不够严谨，甚至有些部分可能是完全错误的，希望大家读的时候可以带着审视的视角，有什么问题可以在下方留言或者直接联系本人（simolark318@gmail.com）

9.26更新：初版没有重视数学公式的一些理论推导与证明，重新从头推导一遍后发现了一些问题，对部分细节内容以及公式进行了修改。

10.15更新：对部分公式进行了重新修改，改正了一些不应该的失误，对比较重要的几个地方重新进行了推导

第一章多臂老虎机（Multi-armed Bandit）问题介绍

问题背景:顺序决策与反馈

多臂老虎机问题是概率论中一个经典问题,属于强化学习的范畴。

设想,一个赌徒面前有N个老虎机,事先他不知道每台老虎机的真实盈利情况,他如何根据每次玩老虎机的结果来选择下次拉哪台或者是否停止赌博,来最大化自己的从头到尾的收益。

我们经常面临一个共同的问题：在有限的资源和不确定的情况下如何做出最佳选择。这种决策通常是序列化的，也就是说，我们不是一次性做出所有决策，而是在一系列的时间点上逐步做出选择。更重要的是，每次选择后，我们都会收到一些反馈，这些反馈可以帮助我们调整未来的策略。这种决策过程的一个核心挑战是如何在探索（尝试新的选项以获取更多信息）和利用（基于已知信息做出最佳选择）之间找到平衡。

问题形式化:多臂老虎机模型

在多臂老虎机问题中，我们面对 $K$ 个不同的臂，每个臂都代表一个可能的决策或行动。当我们选择一个臂时，我们会从与该臂关联的概率分布中获得一个奖励。但这些分布是未知的，我们只能通过尝试不同的臂来逐渐学习这些分布，尝试的越多，我们所知道的信息就越多，越能做出更高收益的选择，的但相应的，也就需要付出更多的资源，因此我们的目标就是在探索和利用之间找到一个平衡点，以获取最大的奖励。

具体来说，我们可以形式化这个问题如下：

臂的集合：有 $K$ 个动作或臂，记为 $\{1, 2, \ldots , K\}$
奖励的概率分布：当在时间 $t$ 选择臂 $i$ 时，我们从一个固定的，但不为我们所知的概率分布 $D_a$ 中得到一个奖励 $r_t$ 。通常假设 $r_t$ 是有界的，例如在 $[0, 1]$ 范围内。

Stochastic MAB

算法的评价指标

这里我们引入一个叫遗憾的概念：

遗憾：在时间 $T$ 的总遗憾值定义为选择最佳臂与策略 $\pi$ 选择的臂之间的差值累积起来的奖励：

R(T) = T \times \mu^* - \sum_{t=1}^T E[r_t]

其中 $\mu^*$ 是最佳臂的平均奖励， $E[r_t]$ 是在时间 $t$ 根据某一策略得到的期望奖励。

在多臂老虎机问题上，我们一般更习惯于用遗憾，即Regert来刻画一个算法的好坏.

更准确的说，我们是用遗憾值的增长速度来刻画算法好坏，比如遗憾值线性增长的算法就不如次线性增长的算法优秀。

而如果采用奖励值的话，无论算法优劣，增长速度都是线性的，所以很难去评估到底哪个算法更优秀。

第二章经典算法介绍

Explore-then-Exploit算法

Explore-then-Exploit

"Explore-then-Exploit" 策略的核心思想是：在初始阶段进行一段时间的探索，之后完全转向利用。这种方法尝试通过首先获取关于每个动作的足够信息，然后选择最佳动作来平衡探索和利用。

基本步骤

探索阶段：在这一阶段，系统均匀地尝试所有的动作，以收集关于每个动作的回报信息。
利用阶段：探索阶段结束后，系统计算每个动作的平均回报，然后持续选择平均回报最高的动作。

例2.1

假设有3个动作：A、B、C，真实的平均回报如下：

A: 0.7
B: 0.8
C: 0.9

但是开始时，我们并不知道这些真实值。为了决定哪个动作是最佳的，我们首先进行探索。例如，我们可能选择每个动作10次：

A: 平均回报 0.68
B: 平均回报 0.82
C: 平均回报 0.89

在探索阶段结束后，我们发现动作C的平均回报是最高的，所以在利用阶段，我们会持续选择动作C。

重点：N的取值

了解了算法基本思想后，我们发现最关键的问题就在于 $N$ 的取值，我们该如何得到一个合适的 $N$ ，使算法的效果能够尽可能好？

在这里定义每个动作 $a$ 的平均奖励为 $\hat{\mu}(a)$ ，我们希望平均奖励能够尽可能接近真实的期望奖励，也就是说我们想要: $\left|\hat{\mu}(a) - \mu(a)\right|$ 的值尽可能小。

在这里定义置信半径(confidence radius)为:

\beta_N = \sqrt{\frac{2\log{T}}{N}}

此时 $\delta = \frac{2}{T^4}$

因为该场景下arm a 每次拉动获得的遗憾值是独立同分布的，那么我们使用霍夫丁不等式 (Hoeffding inequality) 可以得到：

\ P\left\{|\bar{\mu}(a)-\mu(a)| \leq \beta_N\right\} \geq 1-\frac{2}{T^{4}}

我们定义 "good event" 为所有估计值 $\hat{\mu}(a)$ 都接近其真实值 $\mu(a)$ 的情况，即

\epsilon = \{ \forall a \in [k] : | \mu\hat{a} - \mu(a) | \leq \beta_N \}

因此，我们有

P(\epsilon) = 1 - P(\overline{\epsilon}) \geq 1 - \sum_{a=1}^{K} P(| \hat{\mu}(a) - \mu(a) | \geq \beta_N)

又，根据Hoeffding不等式，

P(| \hat{\mu}(a) - \mu(a) | \geq \beta_N) \leq \delta = \frac{2}{T^4}

所以，

P(\epsilon) \geq 1 - K \cdot \frac{2}{T^4}

接下来，让我们首先假设“good event” $\epsilon$ 发生

然后，假设在第二次的利用阶段中，我们没有选择最佳的臂 $\tilde{a}$ ，即 $\tilde{a} \neq a^*$ 。

在good event发生的情况下，我们将说明这并不会有太大影响。

具体来说，在good event $\epsilon$ 发生的情况下，我们有：

- \beta_N \leq \hat{\mu}(\tilde{a}) - \mu(\tilde{a}) \leq \beta_N \quad （good event）

- \beta_N \leq \hat{\mu}(a^* ) - \mu(a^*) \leq \beta_N \quad (best event)

让我们来关注 $\mu(a^* ) - \mu(\tilde{a})$ 的差异，即每步的遗憾:

\mu(a^* ) − \mu(\tilde{a}) ≤ \hat{\mu}(a^* ) + \beta_N − ( \hat{\mu}(\tilde{a}) − \beta_N )≤ 2\beta_N

到这里，我们现在可以将两个阶段的遗憾结合起来:

在第一阶段，每一步最多产生 1 的遗憾，并且有 $KN$ 步。

因此，在 $\epsilon$ ，也就是说“good event”发生的条件下，我们有：

R(T) ≤ KN · 1 + (T − KN) · 2β_N ≤ KN + 2T β_N = KN + 2T · \sqrt\frac{2logT}{N}

因此，要找到最优的 N，我们只需使这两项相等，也就是说，令：

KN = 2T · \sqrt\frac{2logT}{N}

求解得：

N = O(T^{2/3}K^{-2/3}(\log T)^{1/3})

同样的，易求得，

R(T) = O(T^{2/3}(K \log T)^{1/3})

最后，让我们考虑bad event : $\bar{\epsilon}$ ，这种情况发生的概率很低，仅为 $\frac{2K}{T^4}$ 。这时，我们有：

E[R(T)] = E[R(T) | \epsilon] \cdot P(\epsilon) + E[R(T) | \bar{\epsilon}] \cdot P(\bar{\epsilon})\leq O(T^{2/3}(K \log T)^{1/3}) + T \cdot \frac{2K}{T^4} \leq O(T^{2/3}(K \log T)^{1/3})

所以我们得出一条定理：则对任意的 $\delta \in (0,1]$ ,有至少 $1-\delta$ 的自信认为，Explore-then-Exploit算法所产生的遗憾值为：

R(T) = O(T^{2/3}(K \log K)^{1/3})

Epsilon-Greedy算法

Epsilon-Greedy

Epsilon-Greedy算法的基本思想是在每一个时间步，以一定的概率 $\epsilon$ （通常是一个很小的值）随机选择一个动作（探索），或以 $1- \epsilon$ 的概率选择当前已知的最佳动作（利用）。

基本步骤

随机决策：产生一个0到1之间的随机数。如果这个数小于 $\epsilon$ ，则随机选择一个动作；否则，进行贪婪决策。
贪婪决策：选择当前已知的平均回报最高的动作。

例2.2

假设有3个动作：A、B、C。真实的平均回报如下：

A: 0.7
B: 0.8
C: 0.9

在某个时间点，我们基于过去的选择和回报，得知：

A: 平均回报 0.65
B: 平均回报 0.88
C: 平均回报 0.85

如果我们设置的 $ϵ=0.1$ ，那么在90%的时间里，我们会选择动作B，因为它是已知的最佳动作。但在剩下的10%的时间里，我们会随机选择A、B或C中的一个。

显然，这个算法的核心依然在于这个未知数 $\epsilon$ ，如果我们想要得到很好的效果，那么 $\epsilon$ 的取值就十分的重要。

Successive Elimination算法

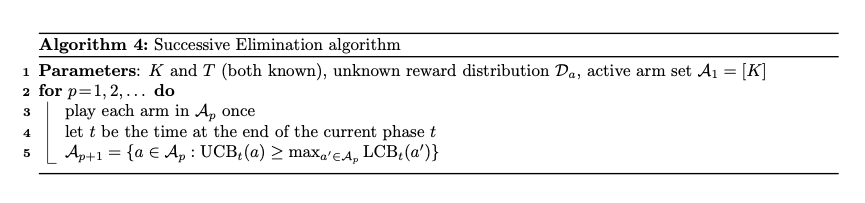
Successive Elimination

Successive Elimination 算法的主要目标是最小化所需的时间步长，以确定哪个动作是最佳的，同时尽可能减少对次优动作的选择。

基本原理

初始化：每个动作都被认为是有潜力的最佳动作。
置信区间：计算每个动作的收益的置信区间。对每条臂a,算法会维护该臂的奖励值的一个置信区间 $[LCB, UCB]$ ,其中:

LCB(lower confidence bound): 经验奖励均值 $μ̂_t(a) - β_t(a)$

UCB(upper confidence bound): 经验奖励均值 $μ̂_t(a) + β_t(a)$

这里 $β_t(a)$ 是置信区间半径,随着臂 $a$ 被拉动的次数 $N_t(a)$ 增大而减小。
消除：在每个阶段p,对活跃臂集合 $A_p$ 中的每条臂a,算法会比较它的UCB与其他臂的LCB。

如果存在臂 $a'$ 使得: $UCB_t(a) < LCB_t(a')$ ，那么就可以认为a不是最优臂,于是可以消除臂a,得到新一轮的活跃臂集合 $A_{p+1}$ 。
选择:在进行决策时,算法只从当前的活跃臂集合 $A_p$ 中选择臂执行,而忽略已经被消除的臂。活跃臂集合中的臂其 $UCB$ 与 $LCB$ 还有重叠,都是潜在的最优臂。

例2.3

假设有5条臂,经过初始探索,得到以下经验奖励均值:

A: $\hat{\mu}_1$ = 0.3
B: $\hat{\mu}_2$ = 0.5
C: $\hat{\mu}_3$ = 0.4
D: $\hat{\mu}_4$ = 0.2
E: $\hat{\mu}_5$ = 0.6

为了简单起见,假设置信区间半径 $β=0.1$ 。

则初始化的活跃臂集合 $A1 = {1,2,3,4,5}$ 。

第1阶段结束时:

$A: [\ 0.2, 0.4 \ ]$
$B: [\ 0.4, 0.6 \ ]$
$C: [\ 0.3, 0.5 \ ]$
$D: [\ 0.1, 0.3 \ ]$
$E: [\ 0.5, 0.7 \ ]$

比较UCB和LCB,可淘汰D,因为: $UCB_D = 0.3 < LCB_B = 0.4$

则第2阶段的活跃臂集合 $A2 = {A, B, C, E}$ 。

重复计算上述步骤，即可快速锁定最优臂,从而可以更多次选择该臂,提高累积奖励。

遗憾值证明

像之前一样，我们首先定义good event为：

\epsilon := \{ \forall a, \forall t, | \hat\mu_t(a) - \mu(a) | \leq \beta_t(a) \}

首先根据算法4，我们知道，对于所有的 $p$ ， $a^*$ 总会存在于活跃集合 $A_p$ 中。

接下来，让我们用反证法来证明这条结论。

首先假设这一点不成立，也就是说，在某一特定阶段t结束时, $a^*$ 会被淘汰。

那么，我们一定对于某个 $a'$ 有：

UCB_t(a^*) < LCB_t(a')

根据UCB和LCB以及good event的定义，我们有：

\mu(a^* ) \leq \hat\mu_t(a^* ) + \beta_t(a^* ) < \hat\mu_t(a') - \beta_t(a) \leq \mu(a')

由上可以得出：

μ(a')>μ(a^* )

但很明显这是不可能的，因为在我们的定义中， $a^*$ 是最优的臂，所以，反例不成立，该结论得证。

现在，我们将说明对于在阶段 $p$ 结束时间 $t$ 的 $A_{p+1}$ 中的每一个臂 $a$ ，都满足

\Delta(a) = \mu(a^* ) - \mu(a) \leq 4\beta_t(a)

直接证明不太好做，那我们就从另一个角度看：

只要任何不满足 $\Delta(a) = \mu(a^* ) - \mu(a) \leq 4\beta_t(a)$ 的条件，也即 $\Delta(a) > 4\beta_t(a)$ 的臂，在时间 $t$ 结束时都会被淘汰，即可说明上式成立。

证明过程如下：

\hat\mu_t(a) + \beta_t(a) \leq \mu(a) + 2\beta_t(a) < \mu(a^* ) - 4\beta_t(a) + 2\beta_t(a) = \mu(a^* ) - 2\beta_t(a^* ) \leq \hat\mu_t(a^* ) - \beta_t(a^* )

因此，我们得到 $\Delta(a) \leq 4\beta_t(a)$ 。

因此我们可以说明，到时间 $t$ 为止, 臂 $a$ 所造成的遗憾是有界的，且满足以下关系：

R(t;a) = N_t(a) \cdot \Delta(a) \leq N_t(a) \times 4 \times \sqrt\frac{log(2KT/\delta)}{2N_t(a)} = O(\sqrt {N_t(a)log(KT/\delta))}

因此，总的遗憾是所有臂 $a$ 的遗憾 $R(t; a)$ 之和：

R(t) = \sum_{a \in [K]} R(t;a) =\sqrt{log(KT/\delta)} \sum_{a} O(\sqrt {N_t(a)}) = O(\sqrt{ KT log(KT/\delta)})

再次提醒： $N_t(a)$ 指的是 $t$ 时刻，arm $a$ 被拉动的次数

因此我们可以得到：对任意的 $\delta \in (0,1]$ ,有至少 $1-\delta$ 的自信认为，Successive Elimination算法可以达到以下的遗憾：

R(T) = O( \sqrt {KT \log(KT/\delta)})

第三章 UCB（Upper Confidence Bound）算法详解

Upper Confidence Bound

我们先回顾一个重要的引理：

对任意的 $\delta \in (0,1]$ ,有至少 $1-\delta$ 的自信认为，对所有臂 $a$ 和时刻 $t$ :

|\hat{\mu}_t(a)-\mu(a)| \leq \beta_t(a) := \sqrt{\frac{\log(2KT/\delta)}{2N_t(a)}}

这里 $\hat{\mu}_t(a)$ 是时刻 $t$ 对臂 $a$ 的均值估计, $N_t(a)$ 是时刻 $t$ 之前针对臂 $a$ 的选择次数。

UCB算法是相比而言在多臂老虎机问题上比较成熟且使用比较多的算法，它展示了一个非常基本的原则——在面对不确定性时持乐观态度。

这里我们回顾一下UCB的定义：

UCB(upper confidence bound):经验奖励均值，计算公式为 $\hat \mu_t(a) + β_t(a)$

为什么UCB与Successive Elimination相比，只维护了获得奖励的上界，而不考虑下界的情况，但却会是一个更好的算法？

因为UCB由两个部分组成，所以这个问题也就可以从两方面来看：

$\hat \mu_t(a)$ 较大：在时间 $t$ ，如果臂 $a$ 有一个较大的 $\hat \mu_t(a)$ ，也就是说此时臂a的奖励值较大，很显然，这是我们想要的。
$\beta_t(a)$ 较大：也就是说， $N_t(a)$ 较小，这意味我们还没有尝试这个臂太多次。

显然，在这种两种情况下，我们都完全有理由去选择拉动臂 $a$ 。

我们可以用一道例题来辅助理解这个算法

例3.1

假设面前有五个臂，每个臂代表一个策略。每次拉动一个臂，会得到一个奖励：1（成功）或 0（失败）。

初始的时候，每个臂都被尝试了一次，得到如下奖励：

A: 1
B: 1
C: 0
D: 0
E: 1

基于UCB算法的选择策略如下：

对于每个臂 i, 计算其 UCB 值
选择 UCB 值最大的臂

当第一次试验结束后，总尝试次数为5。现在我们来为第6次尝试选择一个臂。

A: UCB(A)=1+ $\sqrt{2ln(5)/1}$ =1+1.79=2.79
B: UCB(B)=1+ $\sqrt{2ln(5)/1}$ =2.79
C: UCB(C)=0+ $\sqrt{2ln(5)/1}$ =1.79
D: UCB(D)=0+ $\sqrt{2ln(5)/1}$ =1.79
E: UCB(E)=1+ $\sqrt{2ln(5)/1}$ =2.79

选择 UCB 最高的臂，即可以选择A, B或E。假设我们选择了B并得到了奖励1。现在，B的奖励均值变为(1+1)/2 = 1，且其被尝试次数为2。

继续按照上述策略进行，每次都选择 UCB 值最大的臂。

经过多次迭代，这种策略将确保我们探索所有的臂（保证不会错过真正的最佳臂），同时又能够利用已经获得的信息来获取尽可能多的奖励。

算法分析

得到R(T)的初步范围

对于每一轮 $t$ ，定义： $r_t = \mu(a^*) - \mu(a_t)$ 。

因此： $R(T) = \sum_{t=1}^{T} r_t$

如之前所述，我们定义一个good event $\epsilon$ ：

\epsilon := \left\{ \forall a, \forall t, | \hat\mu_t(a) - \mu(a)| \leq \beta_t(a) \right\}

在good event下，对于 $r_t$ ，我们有：

r_t = \mu(a^* ) - \mu(a_t) = \mu(a^* ) - UCB_t(a^* ) + UCB_t(a^*) - UCB_t(a_t) + UCB_t(a_t) - \mu(a_t) \leq 2\beta_t(a_t)

我们不妨将上式两两一组拆分成3部分：

第一部分： $\mu(a^* ) - UCB_t(a^* ) = \mu(a^* ) - \hat \mu_t(a) - β_t(a)$ 根据good event的定义，我们能知道这一部分是小于等于0的

第二部分： $UCB_t(a^*) - UCB_t(a_t)$ 根据UCB算法，我们知道，我们在每一轮只会选择当前UCB值最大的臂，也即，我们选择的 $a_t$ 的UCB值是所有臂里面最大的，因此这一项也是小于等于0的

第三部分： $UCB_t(a_t) - \mu(a_t)$ 同样根据good event的定义

所以最终得到：

r_t \leq 2\beta_t(a_t)

因此：

R(T) = \sum_{t=1}^{T} r_t \leq \sum_{t=1}^{T} 2\beta_t(a_t) \leq 2 \times \sum_{t=1}^{T} \sqrt { \frac{\log(2KT/\delta)}{2N_t(a_t)} }

整理上式，将与 $t$ 无关的项提出来到求和外面即可得到：

R(T) \leq \sqrt { \log(2KT/\delta)} \times c \times \sum_{t=1}^{T} \sqrt { \frac{1}{N_t(a_t)} }

坐到这里，我们接下来的关键是要去判断这个累加和是否有界，以及是否能得到他的约束范围。

证明累加和有界:

将累加和拆分为对不同的臂a求和:

\sum_{t=1}^T \sqrt{\frac{1}{N_t(a_t)}} = \sum_{a=1}^K \sum_{t: a_t=a} \sqrt{\frac{1}{N_t(a)}}

这里 $t:a_t=a$ 表示在第t轮选择的是臂a的情况。

对于固定的臂a,其被选择的次数 $N_T(a)$ 是确定的。那么我们就可以先对当前选中的臂a被选择的每一轮m求和,

这里的m是从1到 $N_T(a)$ 的值，臂a每被选中一次，m值就加一，直到 $N_T(a)$ ，也即，对于单个的臂a来说，我们先把他所有的m加起来，然后再把所有的臂a加起来，就得到了最终的 $N_t(a_t)$ :

\sum_{a=1}^K \sum_{t: a_t=a} \sqrt{\frac{1}{N_t(a)}} = \sum_{a=1}^K \sum_{m=1}^{N_T(a)} \sqrt{\frac{1}{m}}

这里 $N_T(a)$ 表示在总共T轮里,臂a被选择的次数。

到这一步之后，我们需要判断等式右边的界，这里我们用积分不等式的方法来求，具体如下：

利用积分不等式求边界：

积分不等式：

对于一个正值单调递减的函数f(x)，恒有:

\int_{1}^{n} f(x) dx \geq \sum_{i=1}^{n} f(i)

可以简单画个图来证明一下：

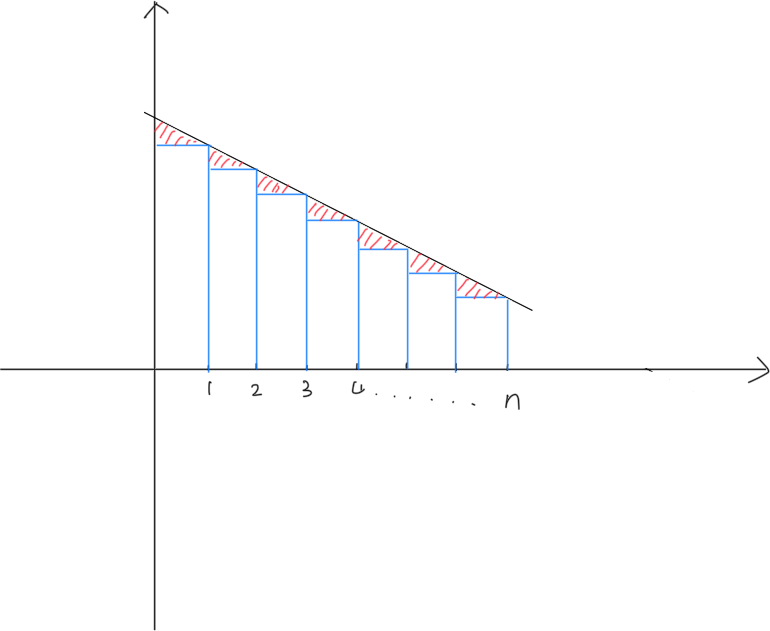
积分代表的是大三角形的面积，而累加则代表一个个小矩形的面积之和，则显然大三角形的面积是大于小矩形的面积和的

回到本题中，我们取 $f(x) = \sqrt{\frac{1}{x}}$ ,则有:

\int_{1}^{N_T(a)} \sqrt{\frac{1}{x}} dx \geq \sum_{m=1}^{N_T(a)} \sqrt{\frac{1}{m}}

计算左侧积分的解,可以得到:

\int_{1}^{N_T(a)} \sqrt{\frac{1}{x}} dx = 2\sqrt{N_T(a)} - 2

为了形式上的简单，在不影响计算的量级的情况下，我们可以做一次放缩，取 $2\sqrt{N_T(a)} - 2 \leq 2\sqrt{N_T(a)}$

带入不等式,当 $c' \geq 2$ 时就可以得到:

\sum_{m=1}^{N_T(a)} \sqrt{\frac{1}{m}} \leq 2\sqrt{N_T(a)} \leq c'\sqrt{N_T(a)}

整理一下，我们有：

\sum_{t=1}^{T} \sqrt{\frac{1}{N_t(a_t)}} = \sum_{a=1}^{K} \sum_{m=1}^{N_T(a)} \sqrt{\frac{1}{m}} \leq c' \sum_{a=1}^{k}\sqrt{N_T(a)} = O(\sqrt{KT} )

最后一个等号需要一些证明技巧，我们把这个求和表示成两个向量的内积，即向量 $a:(1,1,1,1,......,1)$ ，与向量 $b:(\sqrt {N_t(a_1)}, \sqrt {N_t(a_2)},\sqrt {N_t(a_3)} .....,\sqrt {N_t(a_k)})$

我们知道向量 $\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| \times |\mathbf{b}| \times \cos \delta$ , 又 $0 < \cos \delta < 1$

那么很容易得到， $\mathbf{a} \cdot \mathbf{b} \leq |\mathbf{a}| \times |\mathbf{b}|$

那么，就能得到

\sum_{a=1}^k{ \sqrt{N_T(a)}} \leq \sqrt{K \times [ \sum_{a=1}^K N_T(a)]}

显然， $\sum_{a=1}^K N_T(a) = T$ , 所以：

\sum_{t=1}^{T} \sqrt{\frac{1}{N_t(a_t)}} = O(\sqrt{KT} )

那么，像之前的算法一样，我们可以得到这样一条结论：

对任意的 $\delta \in (0,1]$ ,有至少 $1-\delta$ 的自信认为，UCB算法实现的后悔值为：

R(T) = O(\sqrt{KT \log(KT/\delta)})

与问题相关的边界

所有我们之前的求得的边界都被称为最坏情况下的边界或问题无关的边界。

但其实，我们也可以求出和问题有关的边界。

在之前的部分中，我们已经说明过：

\Delta(a_t) = \mu(a^*) - \mu(a_t) \leq 2\beta_t(a_t)

现在让我们聚焦于T轮内某一臂 $a$ 的拉动次数。

对于每个臂 $a$ ，在上述不等式中，我们规定 $t$ 为在 $T$ 轮中臂 $a$ 最后一次被拉动的轮次。然后，我们有：

\Delta(a) \leq 2 \sqrt{\frac{\log(2KT/\delta)}{N_T(a)}}

用 $\Delta(a)$ 来表示 $N_T(a)$ ，即可得到：

N_T(a) = O(\frac{\log(KT/\delta)}{\Delta(a)^2})

因此，我们有如下公式（根据后悔度的定义）：

R(T) = \sum_{a:\Delta(a)>0} \Delta(a) N_T(a) = O\left( \frac{\log(KT/\delta)}{\Delta(a)} \right)

由此，即可再一次提出一条定理：

对于任何 $\delta \in (0, 1]$ ，我们都有至少 $1 - \delta$ 的自信认为：UCB算法将达到的与问题相关的后悔值的界限为：

R(T) = O\left( \frac{\log(KT/\delta)}{\Delta(a)} \right)

第四章 Multi-Armed Bandit问题中的后悔度下界分析

上一章中,我们介绍了Upper Confidence Bound(UCB)算法在Multi-Armed Bandit问题中的应用,并证明了它可以取得 $O(\sqrt{T})$ 的后悔度上界。

一个自然的问题是,这个 $\sqrt{T}$ 的后悔度上界是否是最优的?是否存在其他更好的算法可以取得比 $\sqrt{T}$ 量级更小的后悔度上界?

为了回答这个问题,我们需要从另一个方向入手——也就是探讨Multi-Armed Bandit问题的后悔度下界。

若可以证明任何算法的后悔度下界都是 $\sqrt{T}$ , 那么就可以断定UCB算法是最优的,无法通过设计新的算法再取得进一步改进。

问题形式化

设 $Alg$ 表示所有可能的Bandit算法的集合, $P$ 表示问题实例的集合。

则对于任意算法 $A∈Alg$ ,在问题实例 $P$ 上的 $T$ 轮期望后悔度表示为: $E_A[\bar{R_T}(A,P)]$ ，则我们定义任一算法在最坏情况下的期望后悔度为:

R^* = \min_{A∈Alg} \max_P E_A[\bar{R_T}(A,P)]

也就是说,我们想要找到一个算法A, 使得在最坏的问题实例P上,它的后悔度尽可能小。

$R^*$ 就是在 $Alg$ 中找出的最优算法在最坏情况下可以取得的后悔度。

也即，我们的目标就是证明 $R^*$ 的下界是 $Ω(\sqrt T)$ 。

证明思路

为了证明后悔度的下界,我们将运用最小化最大值原理:

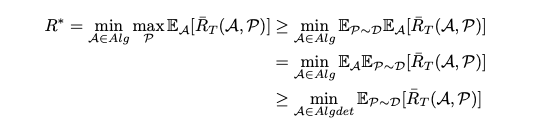
也就是说,如果我们可以构造一个问题分布D,使得在这个分布下,任意确定性算法A的期望后悔度有下界,那么就可以推出最坏情况下的后悔度下界。

因此,我们的技术路线是:

构造一个“困难”的问题分布D
证明在分布D下,任意确定性算法A的期望后悔度有 $Ω(\sqrt{T})$ 的下界

通过姚氏定理, 我们就可以得到最坏情况下后悔度的下界。

双臂情况下的简单证明

我们先证明只有两个臂的简单的情况，然后总结规律再扩展至多臂：

我们选取一个臂作为最优臂，它的平均奖励为 $1/2+\epsilon$ ，同时另外一只是 $1/2$ 。为了区分这两个臂，我们需要让估计误差小于 $\epsilon$ 。

我们知道，根据霍夫丁不等式，误差将以 $1/\sqrt n$ 的速率衰减。

那么，样本量 $n$ 就必须满足 $1/\sqrt{n} < \epsilon$ ,即我们要求误差的衰减速率小于 $\epsilon$ 。如果估计误差大于或等于ϵ，那么我们可能会错误地选择次优的臂，因为我们无法确定观察到的差异是由于真正的期望收益之间的差异还是由于估计误差引起的。

所以易得， $n > \frac {1}{\epsilon^2}$

也就是说人们必须至少拉动次优臂 $\frac {1}{\epsilon^2}$ 次

而每选择一次次优臂，就至少会产生 $\epsilon$ 的遗憾

那么，总遗憾就至少为 $\frac {1}{\epsilon^2} \times \epsilon = \frac{1}{\epsilon}$ 。

如果我们选择 $\epsilon = \frac{1}{\sqrt T}$ ，那么遗憾将至少为 $Ω( \sqrt T)$ 。

（⚠️：若 $\epsilon$ 选择的太小，那么需要拉动的次数会超过T，于实际场景而言就没有任何意义了）

现在，基于这个双臂的简单示例，我们将正式构建一个问题类的分布。

构造问题分布

在K个arm中,均匀随机选择一个arm作为best arm,它的平均奖励为 $1/2+ε$ 。其余K-1个arm的平均奖励都是 $1/2$ 。

也就是说,我们随机生成K个可能的问题实例,每个实例中都有一个唯一的best arm。然后D就是均匀在这K个实例上的分布。

分析确定性算法的后悔度

固定一个确定性算法 $A$ ,我们来分析它在分布 $D$ 上的期望后悔度:

我们定义 $E_{P \sim D}[\bar{R_T}(A,P)]$ 如下：

E_{P \sim D}[\bar{R_T}(A,P)] = \frac{1}{K} \sum_{a=1}^{K} E_a(R_T)]

我们先计算 $E_a(R_T)$

E_a(R_T) = E_a[\sum_{t=1}^{T}[\mu(a^* ) - \mu(a_t)]]

由已知， $\mu(a^* ) = 1/2 + \epsilon$ , 当选择的是最优臂是 $a_t = 1/2 + \epsilon$ , 否则， $a_t = 1/2$

对任意arm $a$ , 我们在这里定义 $N_a$ 表示在 $T$ 轮中算法 $A$ 选择该arm的次数。

那么我们就可以整理得

E_a(R_T) = E_a(\epsilon \times (T - N_a ))

那么也就是说

E_{P \sim D}[\bar{R_T}(A,P)] = \epsilon \times [T - (1/K) \sum_{a=1}^{K} E_a(N_a)]

既然我们的目标是证明上式的下界。那么问题的关键就是要分析 $E_a[N_a]$ 的上界。

这里我们先引入一个中间桥梁项： $E_0(N_a)$ , 表示当没有选择特殊臂时,算法A选择臂a的期望次数，这个参数的引入使得我们可以连接 $E_a[N_a]$ 和 $KL$ 散度之间的关系。

基于这个，我们就能得到：

E_a[N_a] - E_0[N_a] = \sum_{(r_{1:T})} (N_a(P_a(r_{1:T})) - N_a(P_0(r_{1:T})))

这里求和是对所有可能的奖励序列 $r_{1:T}$ 的统计。 $P_a$ 和 $P_0$ 分别表示选择了特殊臂a时和没有选择特殊臂时的奖励分布。

对公式进行重新整理，可以得到:

\sum_{(r_{1:T})} (N_a(P_a(r_{1:T})) - N_a(P_0(r_{1:T}))) = N_a \times \sum_{r_{1:T}}(P_a(r_{1:T}) - P_0(r_{1:T}))

因为 $N_a \leq T$ ， $\sum_{r_{1:T}}(P_a(r_{1:T}) - P_0(r_{1:T})) = |P_a - P_0|_1$

所以，我们有：

E_a[N_a] - E_0[N_a] \leq T|P_a - P_0|_1

使用Pinsker不等式,有:

|P_a - P_0|_1 \leq \sqrt{2KL(P_a||P_0)}

整理后，易得:

E_a[N_a] - E_0[N_a] \leq T\sqrt{2KL(P_a||P_0)}

这里需要引入一条定理：

对于任意分布 $P$ 和 $Q$ ,以及一个随机变量 $X$ 取值在集合{ $1,2,...,K$ }上,有:

KL(P||Q) \leq \sum_{j=1}^K E_Q[N_j] \times KL(Q(\cdot|X=j)||P(\cdot|X=j))

如果不知道的话，我们在这里介绍一下 $KL$ 散度的计算公式：

KL(P||Q) := \sum_y P(y)log [ \frac{ P(y) }{ Q(y) } ]

回到我们的问题中来，我们很容易发现，对于不是特殊臂 $a$ 的臂 $j$ ,有:

P_0(·|j) = P_a(·|j)

因为这些臂上的分布在 $P_a$ 和 $P_0$ 下是相同的。

换句话说，只有当 $j = a$ 时， KL项才可能不为0

将这个观察整理代入, 我们有:

KL(P_a||P_0) \leq E_0[N_a] KL(P_0(\cdot|a)||P_a(\cdot|a))

可以计算出这个 $KL$ 散度值为:

KL(P_0(\cdot|a)||P_a(\cdot|a)) = (1/2)\log( \frac{1/2}{(1/2+\epsilon}) + (1/2)\log( \frac{1/2}{(1/2-\epsilon})\ = (1/2)\log( \frac{1}{1-4\epsilon^2})

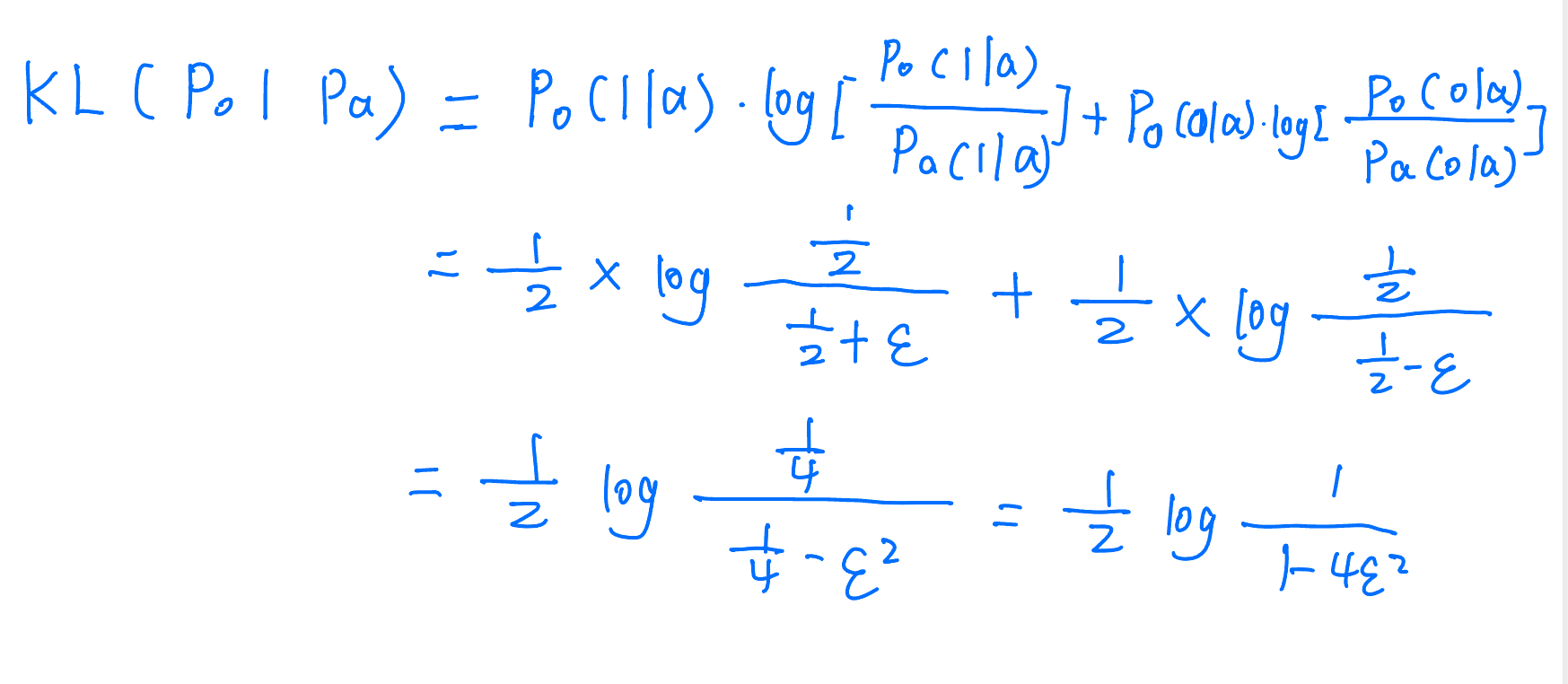
那么，让我们回到之前的式子:

E_a[N_a] - E_0[N_a] \leq T\sqrt{2KL(P_a||P_0)}

那么：

E_a[N_a] \leq E_0[N_a] + T\sqrt{2KL(P_a||P_0)}

现在，我们对方程的两边同时求和，即得：

\sum_a E_a[N_a] \leq \sum_a E_0[N_a] + T \times \sqrt{log( \frac{1}{1-4ε^2})} \times \sum_a \sqrt{E_0(N_a)}

易得， $\sum_a E_0(N_a) = T$ , 因为没有特殊臂时每条臂的期望次数总和为 $T$

而对于没有特殊臂的情况，每个臂的 $E_0(N_a)$ 其实是固定的，为 $T/K$ ，所以

\sum_a \sqrt{E_0(N_a)} = K \times \sqrt {T/K}

所以能得到如下的公式

\sum_a E_a[N_a] ≤ T + T\sqrt{log( \frac{1}{1-4ε^2})} \sqrt{KT}

带入后悔度公式,可以得到在分布D下,算法A的期望后悔度是 $Ω(\sqrt{T})$ 。

至此,通过姚氏定理即完成了证明任意算法在最坏情况下的后悔度下界是 $Ω(\sqrt{T})$ 。这证明了UCB算法是最优的,它的 $\sqrt{T}$ 上界无法再被打破。

参考文献

ECE7995: Online Decision Making [https://sites.google.com/view/ece7995/home] Lecture 13-15
多臂老虎机导论(二)Stochastic Bandits [https://blog.csdn.net/weixin_39059031/article/details/105690221]
强化学习理论基础 4.1 Bandit简介与遗憾分解引理 (Bandits, Regret Decomposition Lemma) [https://www.bilibili.com/video/BV18F411e7QR/]

目录

前言

第一章多臂老虎机（Multi-armed Bandit）问题介绍

问题背景:顺序决策与反馈

问题形式化:多臂老虎机模型

算法的评价指标

相关前置知识

霍夫丁不等式(Hoeffding’s inequality)

姚氏定理

第二章经典算法介绍

Explore-then-Exploit算法

基本步骤

例2.1

重点：N的取值

Epsilon-Greedy算法

基本步骤

例2.2

Successive Elimination算法

基本原理

例2.3

遗憾值证明

第三章 UCB（Upper Confidence Bound）算法详解

例3.1

算法分析

得到R(T)的初步范围

证明累加和有界:

将累加和拆分为对不同的臂a求和:

利用积分不等式求边界：

与问题相关的边界

第四章 Multi-Armed Bandit问题中的后悔度下界分析

问题形式化

证明思路

双臂情况下的简单证明

构造问题分布

分析确定性算法的后悔度

参考文献

目录

前言

第一章 多臂老虎机（Multi-armed Bandit）问题介绍

问题背景:顺序决策与反馈

问题形式化:多臂老虎机模型

算法的评价指标

相关前置知识

霍夫丁不等式(Hoeffding’s inequality)

姚氏定理

第二章 经典算法介绍

Explore-then-Exploit算法

基本步骤

例2.1

重点：N的取值

Epsilon-Greedy算法

基本步骤

例2.2

Successive Elimination算法

基本原理

例2.3

遗憾值证明

第三章 UCB（Upper Confidence Bound）算法详解

例3.1

算法分析

得到R(T)的初步范围

证明累加和有界:

将累加和拆分为对不同的臂a求和:

利用积分不等式求边界：

与问题相关的边界

第四章 Multi-Armed Bandit问题中的后悔度下界分析

问题形式化

证明思路

双臂情况下的简单证明

构造问题分布

分析确定性算法的后悔度

参考文献

第一章多臂老虎机（Multi-armed Bandit）问题介绍

第二章经典算法介绍